在上一节内容中,我们初步了解了深度学习的一些概念,但文字总是抽象的,这一节内容我们使用一个简单的例子对各个概念进行一些更细致的理解。
实例描述:假设某学校周边有一个餐厅,餐厅有过去十年每一天的销售额,现在要实现一个深度学习算法,推算下一天的销售额。
根据上一节的知识,我们需要根据餐厅过去十年的数据训练一个深度学习模型,再使用最近数据进行推理,即可预测下一天的销售额。
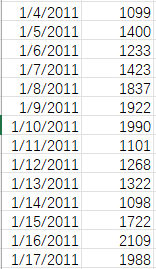
0x01 设计原始网络
首先我们设计一种算法,该算法用于确定数据集数据和目标数据的关系,现在我们并不明确这种关系,先使用一种最简单的算法:认为下一天的销售额只和上一天的有关,并且是线性关系,即:
y=wx+b
在这个简单的算法中,w即权重,b即偏置。
0x02 设计损失函数
损失函数用来计算所有计算结果和实际结果的差距,在该实例中,设e=|y‘ – y|,即预测值与实际值差的绝对值,则损失
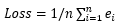
即每一次差距的绝对值之和。
0x03 优化器与梯度下降
优化器即我们如何使用loss值对W和B进行修正,我们可以自己设计规则,比如自己设计W和B进行增加或减少的操作,逐步达到loss最小的目标。
在该问题的数值回归场景中,通常会使用到Optimization(梯度下降)的方法对Loss值进行阶梯回归,使其达到最优解。所谓损失函数的梯度,实际就是对w和b求偏导,梯度下降算法的过程常被形象地形容为”上山“”下山“,如下图中Loss曲线一般,顺着曲线往上则为”上山“过程,顺着曲线向下滑则为”下山“过程。当选取不同的w或b值时,得到不同的loss值和在该点的偏导。
何为下山(梯度下降)呢?即是当我们假设一个w和b的值,我们得到了一个高度(loss)和当前的坡度(梯度向量),此时我们无法得知该高度到底在山的什么位置,我们只能根据坡度(梯度向量),选择向下走(梯度下降),假设我们定下一个目标:每次走五公里重新计算一次(梯度步长),此时可得到一个新的高度和坡度,再次判断,直到最低点为止。
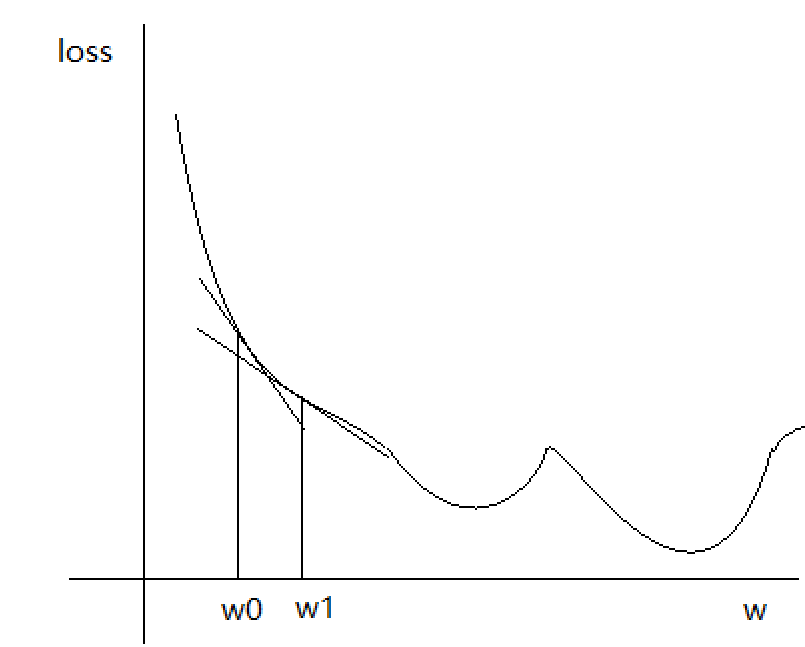
这里我们得到了新的概念:梯度步长。即每一次进行下降的步长大小(图中w0到w1的距离),通常由学习率进行控制。
在该示例中:
假设第一次设w为1.3,b为500,学习率0.1,代入计算损失为8000,梯度向量为-10;
计算得到第二次w为1,b为400,学习率0.1,代入计算损失为3000,梯度向量为-4;
计算得到第三次w为0.87,b为300,学习率0.1,代入计算损失为4000,梯度向量为1;
此时发现损失值较上一次增大,说明步长跨的太大(下山一次走太多了,错过最低点了),此时将学习率降低为0.05,重新进行第三次计算 . . .
由此循环往复,使w和b的值一步步贴近最佳值,使损失值收敛。
在此之前,我们还应该设计了梯度下降停止的条件,例如学习率小于0.01,或者计算100次后自动停止等等。
0x04 优化算法
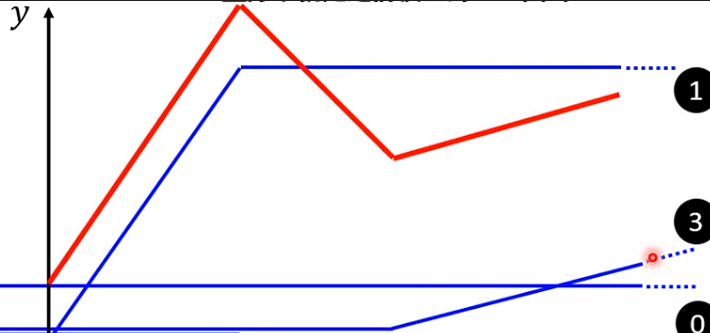
在找到最优值时,第一次训练就结束了,最终得到的参数为y=0.97x+366,最小损失值为2600,使用该模型和当前销售额即可对后一天销售额进行推理,将多次推理与实际值的对比作图可得到以下图像:
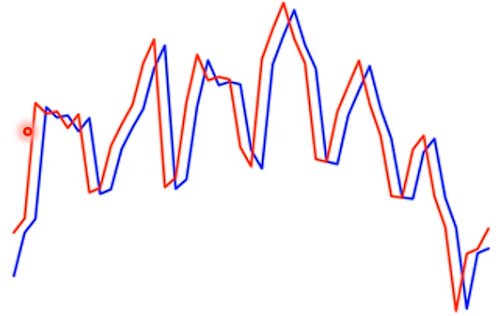
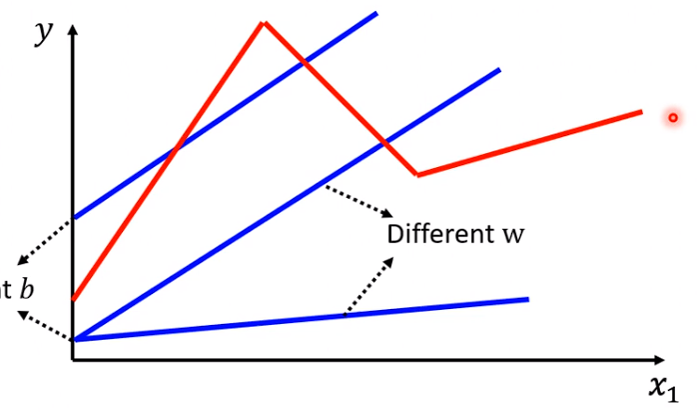
其中,红色图像为真实销售额,蓝色图像为预测值。观察该图像可发现一个较为明显的问题:蓝色预测曲线的预测可以说基本都不准确,看起来曲线贴近是因为预测使用了前一天的数据,本来要得到的结果是蓝色预测,红色跟着蓝色曲线走,现在情况反了过来。
这种情况是明显的没有得到预测效果,其原因也很明显,从图像可以看出,当天销售额并非是只跟前一天的销售额有关系,而是呈现周期性的增长与减退,仔细观察不难发现:销售额变化周期和一周的时间刚好挂钩,周内销售额很高,周末跌到最低。那么算法的优化路线就很明显了:将至少每7天的值纳入下一天的预测依据。
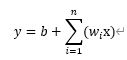
再次计算得到最小损失值:2000。
0x05 激活函数
进行了初步优化后,损失值却是得到了优化,但是结果仍然很差,不具备指导意义,其原因是什么呢?其实观察真实值的曲线图便可知道,实际值的曲线是一个类似信号曲线的周期性曲线,而我们使用了一个或多个线性函数去拟合该曲线,无论如何调整参数,该曲线都不可能较完美地贴合该曲线:
该如何做呢?很明显,我们需要使用非线性的函数去拟合,例如Sigmoid:
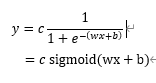

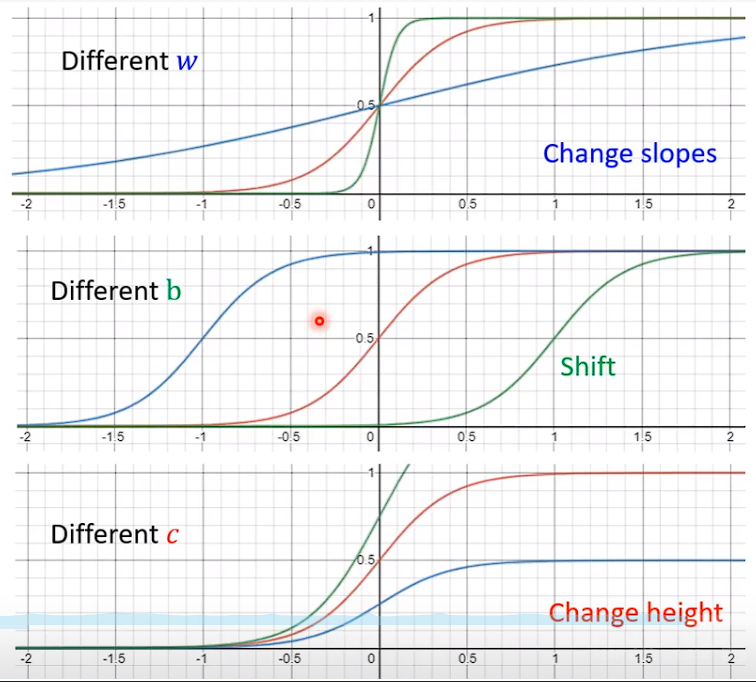
使用该方式设计新的基本模型:
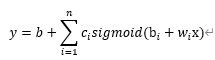
取至少七天的优化版本:
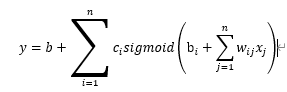
将公式中的sigmod参数展开用r进行表示:

整个公式展开:

梯度下降方法,按梯度计算每个b和w的微分,这样的微分集合称为gradient,然后用微分梯度计算b和w的下降,再次代入计算:

在该示例中:
假设使用3个sigmoid逼近目标函数,则i=3,使用连续七天的值作为推断依据,则j=7;则θ一共包含3个b和21个w一共24个参数,使用梯度下降的方法对24个参数进行逐步优化得到最后最小损失值:1400。
该模型优化完毕。